Understanding The Area Of A Square: Your Simple Guide

This idea of area, it's basically about how much flat surface something takes up. For a square, which is a shape with four equal sides and four perfect corners, finding this space is actually quite straightforward. My text, for instance, talks about how the formula for the area of a square is a lot like other area formulas, just a bit special for squares. It's all about counting the little squares that would fit inside, more or less.

In this article, we'll walk through what the area of a square truly means. We'll look at the very simple formula used to calculate it, and we'll even try out some examples together. We'll also touch on why this bit of math is important and how it connects to other shapes. So, get ready to get a good grip on the area of a square; it's honestly not that hard.

• Susan Collins Net Worth
• The Rock Net Worth 2024
• Lil Bow Wow Net Worth

Table of Contents

• What Exactly Is the Area of a Square?
• The Simple Formula for Square Area
• Why Side Times Side? A Quick Look
• Putting the Formula to Work: Examples
  • Example 1: A Basic Calculation
  • Example 2: A Real-World Situation
• Finding Area When You Only Know the Perimeter
• Area vs. Perimeter: What's the Difference?
• Why Knowing the Area of a Square Matters
• What About Irregular Shapes?
• Frequently Asked Questions (FAQs)
• Wrapping Things Up

What Exactly Is the Area of a Square?

The area of a square, you see, is all about the flat space it covers. Think of it like this: if you had a square-shaped piece of paper, the area would be how much paper there actually is. My text describes it as "the number of unit squares needed to fill in a square." This means we're measuring how many little, perfectly square units, like one-inch by one-inch squares, would fit inside the bigger square without any gaps or overlaps. It's a way to measure the size of a two-dimensional surface, more or less.

It's simply defined as the space occupied by the square. So, if you draw a square on a piece of graph paper, the area is basically the count of all those tiny squares inside its boundary. This concept is pretty fundamental to understanding space in geometry, you know? It helps us quantify surfaces, which is actually quite handy.

The area of a square is the space contained within its perimeter. Imagine a fence around a square garden. The perimeter is the length of that fence, but the area is all the dirt and plants inside the fence. The grey space in a figure often represents the area of the square, showing you just how much ground it covers, or so it seems. This measurement is always given in "square units," like square inches, square meters, or square feet, because we are, after all, counting little squares.

• Kylie Minogue Net Worth
• Joel Olsteens Net Worth
• Net Worth Of Tina Turner

The Simple Formula for Square Area

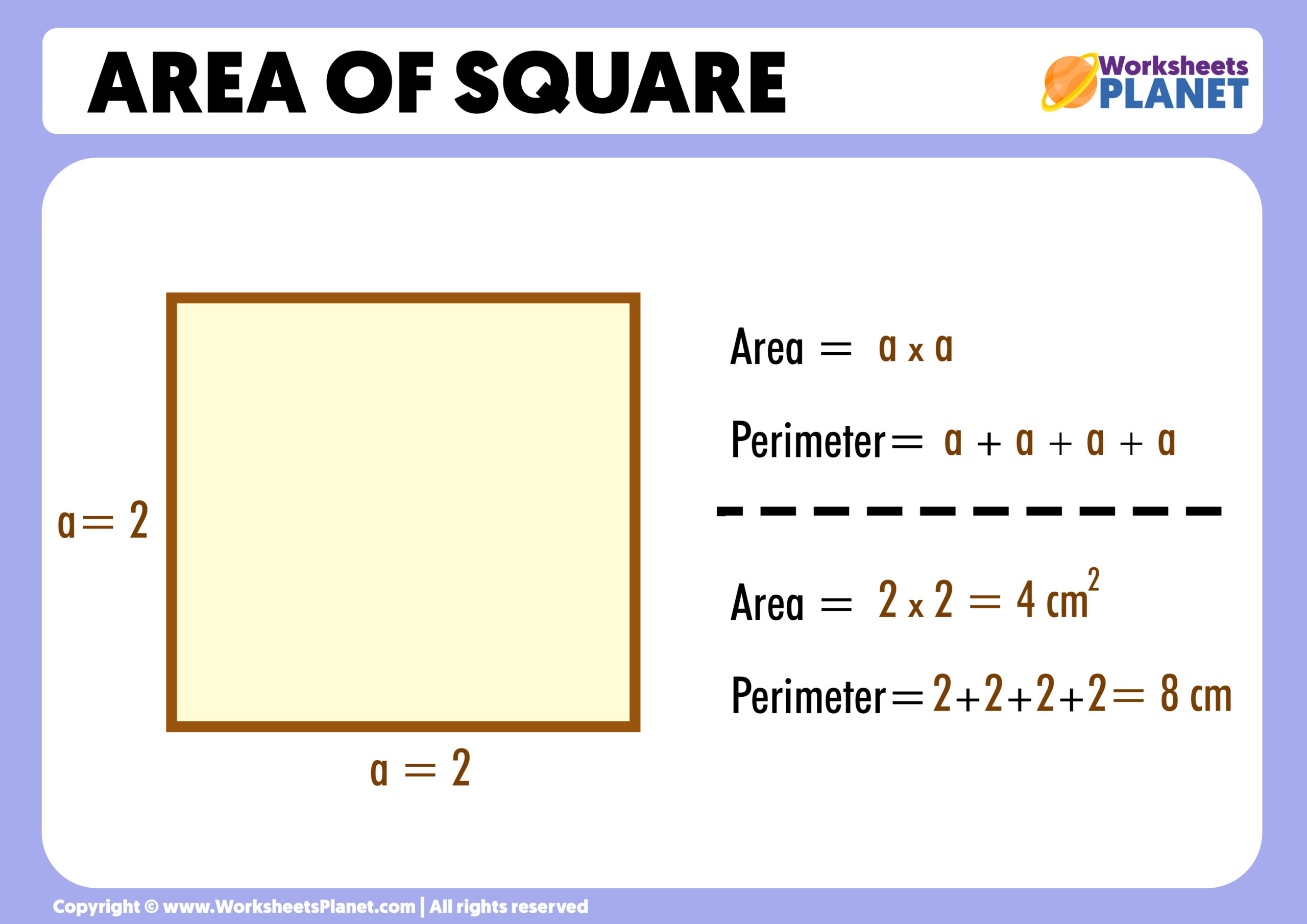
Now, for the really good part: how do you actually calculate this area? Well, my text makes it pretty clear. It says, "The area of a square is defined as the number of square units that make a complete square. It is calculated by using the area of square formula, Area = side × side." This formula is honestly quite straightforward. You just need to know the length of one side of the square, and that's it.

Since a square has four sides that are all the exact same length, you only need to measure one of them. Let's say the length of one side is 's'. Then, the formula becomes: Area = s × s, or as it's often written, Area = s². This means you're multiplying the side length by itself, or "squaring" the side. It's a very neat way to do it, truly.

My text also mentions, "To find the area of a square, use the formula a = side^2, where side is the length of one of the sides of the square." This confirms that 'a' stands for area, and 'side' is just the length we're talking about. So, if a side is 5 units long, the area would be 5 times 5, which is 25 square units. It's almost that simple.

Why Side Times Side? A Quick Look

You might wonder why it's "side times side." Why not something else? Well, think back to those little unit squares we talked about. If you have a square that is, say, 3 units long on each side, you can imagine lining up 3 unit squares along one edge. Then, you can make 3 such rows. So, you have 3 rows of 3 squares each, which gives you a total of 3 × 3 = 9 unit squares. This is precisely why the formula works, you know?

This concept is also why area is measured in "square units." When you multiply a length by a length, you get a square measurement. For example, if your side is in centimeters, then side × side gives you square centimeters (cm²). If it's in meters, you get square meters (m²). It's a very logical system, in a way.

My text hints at this too, mentioning "the area of a square is the product of its..." implying the sides. It's a fundamental concept in geometry, actually, and once you grasp this visual, the formula just makes perfect sense. It's basically a shortcut for counting all those tiny squares, so.

Putting the Formula to Work: Examples

Let's try a couple of examples to see how this works in practice. It's often easier to get a feel for things when you apply them, right? These examples will show you just how simple it can be.

Example 1: A Basic Calculation

Imagine you have a square-shaped coaster, and you measure one of its sides. Let's say it measures 10 centimeters. How much surface area does this coaster cover?

Here's how you'd figure it out:

1. **Identify the side length:** The side (s) is 10 cm.
2. **Apply the formula:** Area = s × s
3. **Calculate:** Area = 10 cm × 10 cm = 100 cm²

So, the coaster covers 100 square centimeters of space. Pretty neat, isn't it? This calculation is very typical for finding the area of a square.

Example 2: A Real-World Situation

Suppose you're planning to lay new sod in a perfectly square patch of your garden. You measure one edge of the patch, and it's 8 meters long. How much sod do you need to buy?

Let's break this down:

1. **Side length:** The side (s) is 8 meters.
2. **Area formula:** Area = s × s
3. **Calculation:** Area = 8 m × 8 m = 64 m²

You would need 64 square meters of sod to cover that garden patch. This shows how knowing the area can help with practical projects, you know? It's really quite useful.

Finding Area When You Only Know the Perimeter

What if you don't know the side length directly, but you know the perimeter of the square? My text mentions, "If you only know the perimeter of the square, you can find the..." This is a slightly different situation, but still very doable. The perimeter of a square is the total length of all its sides added together. Since all four sides are equal, the perimeter is simply 4 times the length of one side (Perimeter = 4 × s).

So, if you know the perimeter, you can actually work backward to find the side length. You would just divide the perimeter by 4. For example, if the perimeter of a square is 20 meters, then each side must be 20 meters / 4 = 5 meters. Once you have the side length, you can then use the area formula (Area = s²) to find the area. In this case, Area = 5 m × 5 m = 25 m². It's a two-step process, but still very manageable, apparently.

My text also says, "Learn how to find the perimeter from the area of a given shape," which is the reverse of what we just did, but it highlights the connection between these two measurements. It's all part of understanding how these shapes work, so.

Area vs. Perimeter: What's the Difference?

It's pretty common for people to mix up area and perimeter, but they are actually very different concepts. My text explains, "The area of a square is the space contained within its perimeter." This is a great way to put it. The perimeter is the distance around the outside edge of a shape, like walking along the boundary of a square field. It's a one-dimensional measurement, usually given in units like meters or feet. Think of it as the length of a fence.

Area, on the other hand, is the amount of surface inside that boundary. It's a two-dimensional measurement, always given in square units. Think of it as the amount of grass inside that fenced field. So, while both describe aspects of a shape's size, they measure completely different things. It's a subtle but important distinction, you know?

My text also references "Learn how to calculate the area of a square or a rectangle," and then separately mentions "Learn how to find the perimeter from the area of a given shape." This separation in the text suggests they are distinct but related concepts, which they are. Understanding both is really key to working with shapes, so it's almost vital.

Why Knowing the Area of a Square Matters

Knowing how to calculate the area of a square isn't just for school assignments; it has many real-world applications. For instance, if you're buying carpet for a square room, you'll need to know the room's area to buy the right amount. Similarly, if you're painting a square wall, the paint quantity you need depends on the wall's area. It's really quite practical.

Farmers might use it to calculate the size of a square plot of land for planting. Architects and builders use area calculations all the time for planning spaces, estimating materials, and designing structures. Even in crafts, like quilting or making square picture frames, understanding area helps you manage your materials efficiently. It's a skill that pops up in many places, actually.

The concept of area extends beyond just squares, too. My text mentions, "Learn how to calculate the area of a square or a rectangle." The principles you learn with squares can often be applied or modified for other shapes, making this a foundational piece of knowledge. It's a building block for more complex geometry, you know?

What About Irregular Shapes?

While we're focusing on squares, it's worth a quick mention that not all shapes are perfectly square or rectangular. My text touches on this, saying, "How do you find the area of irregular shapes? When dealing with irregular shapes, finding the area requires dividing the figure into known shapes that have an area formula." This is a pretty clever strategy.

So, even if a shape isn't a simple square, you can often break it down into smaller, simpler shapes like squares, rectangles, or triangles. Then, you calculate the area of each of those smaller, regular shapes and add them all up. This way, the basic understanding of square area becomes a tool for tackling more complicated figures. It's a good problem-solving approach, really.

Frequently Asked Questions (FAQs)

People often have a few common questions about the area of a square. Let's try to clear some of those up, too. It's good to get all your questions answered, right?

What is the area of a square?

The area of a square is the total amount of flat surface or space enclosed within its four equal sides. It's like measuring how much floor space a square rug takes up, you know? It's always measured in square units, such as square inches or square meters.

How do you calculate the area of a square?

To calculate the area of a square, you use a very simple formula: you multiply the length of one side by itself. So, if 's' is the length of a side, the formula is Area = s × s, or Area = s². For example, if a side is 7 units long, the area is 7 × 7 = 49 square units. It's pretty straightforward, really.

Can you find the area of a square if you only know the perimeter?

Yes, you absolutely can! First, you need to find the length of one side. Since a square has four equal sides, you just divide the perimeter by 4. Once you have the side length, you can then use the standard area formula (side × side) to find the area. It's a two-step process, but it works every time, you know?

Wrapping Things Up

So, there you have it: the area of a square. It's a fundamental concept in geometry, and as we've seen, it's pretty simple to grasp. Whether you're a student learning the basics or an adult trying to figure out a home project, knowing how to calculate the space a square occupies is a really handy skill. My text clearly outlines that it's simply the product of its side multiplied by itself, which is a very clear way to put it.

Understanding this concept also opens the door to understanding the area of other shapes, and even how to tackle more complex, irregular figures by breaking them down. It’s a foundational piece of math that sticks with you. So, keep practicing, and you'll find yourself using this knowledge in all sorts of unexpected ways, you know? It's a good skill to have, truly.

Learn more about shapes and measurements on our site, and link to this page here for more general information about area in mathematics.